IS-LMモデルは，財市場（IS曲線）と貨幣市場（LM曲線）の均衡を同時に捉えることで， 短期における国民所得（$Y$）と利子率（$r$）の関係を示すマクロ経済モデルである． 本モデルは，1937年にジョン・R・ヒックス（J.R. Hicks）によって提唱され，ケインズ経済学を数理的に整理するうえで大きな役割を果たした．

財市場の均衡は以下の恒等式で表される：

$$Y = C(Y - T) + I(r) + G$$

ここで，消費 $C$ は可処分所得に依存し，投資 $I$ は利子率 $r$ に反比例する． 利子率が低下すると投資が増加し，それによって国民所得 $Y$ も増加するため，IS曲線は右下がりとなる．

貨幣市場の均衡は次の式で示される：

$$\frac{M}{P} = L(Y, r)$$

名目貨幣供給 $M$ は中央銀行によって決定され，物価水準 $P$ は短期において固定されていると仮定する． 貨幣需要 $L$ は所得 $Y$ に比例し，利子率 $r$ に反比例する． 所得が増加すると貨幣需要も増加するため，均衡のためには利子率が上昇し，LM曲線は右上がりとなる．

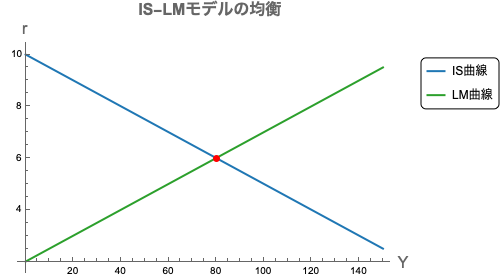
IS曲線とLM曲線の交点は，国民所得と利子率の同時均衡点（$Y^*$，$r^*$）を示す． これは，財市場と貨幣市場の両方が均衡している状態である．

IS-LMモデルは，財政政策や金融政策の効果を分析するツールとして活用される． たとえば，財政支出の増加（$G↑$）や減税（$T↓$）はIS曲線を右方に移動させ，金融緩和（$M↑$）はLM曲線を右方にシフトさせる．

ジョン・R・ヒックスは1937年の論文「Mr. Keynes and the Classics」において，ケインズ理論を図式的に表現するためにIS-LMモデル（当時はIS-LL）を提案した． これにより，ケインズと古典派の枠組みが比較され，ケインズ経済学の理論的普及に貢献した． この業績を含め，彼は1972年にノーベル経済学賞を受賞している．

IS-LMモデルは短期の物価固定を前提としており，供給側の分析を含んでいない． したがって，現代ではIS-LM-ASモデルやDSGEモデル（動学的一般均衡モデル）などに発展している．

\[\text{（消費関数）} \quad C = 100 + 0.8(Y - T) \tag{1}\] \[\text{（投資関数）} \quad I = 200 - 10r \tag{2}\] \[\text{（政府支出）} \quad G = 200 \tag{3}\] \[\text{（税）} \quad T = 100 \tag{4}\] \[\text{（貨幣需要関数）} \quad L = 0.25Y - 20r \tag{5}\] \[\text{（貨幣供給）} \quad M = 400 \tag{6}\] \[\text{（価格水準）} \quad P = 1 \tag{7}\]

IS曲線の導出

(1)，(2)，(3)，(4)より，財市場の均衡は以下のように書ける． \[ Y = C + I + G = 100 + 0.8(Y - 100) + (200 - 10r) + 200\tag{8} \] 展開すると， \[ Y = 100 + 0.8Y - 80 + 200 - 10r + 200 = 0.8Y + 420 - 10r \] \[ 0.2Y = 420 - 10r \Rightarrow Y = 2100 - 50r \] となる．したがって，IS曲線は以下のように表される： \[ Y = 2100 - 50r\tag{9} \]

LM曲線の導出

(5)，(6)，(7)より，貨幣市場の均衡は以下のように書ける． \[ \frac{M}{P} = 0.25Y - 20r \Rightarrow 400= 0.25Y - 20r\tag{10} \] 展開すると， \[ Y = 1600 + 80r\tag{11} \] となる．

IS曲線とLM曲線の交点（均衡点）

均衡は IS = LM の交点として求められる．(8)，(9)より， \[ 2100 - 50r = 1600 + 80r \] \[ 500 = 130r \Rightarrow r = \frac{500}{130} \approx 3.85 \] と計算できる． この値をIS曲線（(8)）に代入して \( Y \) を求めると， \[ Y = 2100 - 50 \cdot 3.85 \approx 1907.5 \] となる．

均衡点の結論

したがって，IS-LMモデルにおける均衡は， \[ r^* \approx 3.85,\quad Y^* \approx 1907.5 \] と計算できる．

Mathematicaのプログラム

📋 コピー

(*パラメータ設定*)
T = 100;
G = 200;
M = 400;
P = 1;

(*関数定義*)
Cons[Y_] := 100 + 0.8 (Y - T);
Inv[r_] := 200 - 10 r;
L[Y_, r_] := 0.25 Y - 20 r;

(*IS曲線:Y=C+I+G を rについて解く\[RightArrow]r=f(Y)*)
isEq = Y == Cons[Y] + Inv[r] + G;
isSol = Solve[isEq, r][[1]];  (*r->... の形*)

(*LM曲線:L(Y,r)=M/P を rについて解く\[RightArrow]r=f(Y)*)
lmEq = L[Y, r] == M/P;
lmSol = Solve[lmEq, r][[1]];  (*r->... の形*)

(*交点を数値で求める*)
intersection = 
  Solve[{Y == Cons[Y] + Inv[r] + G, L[Y, r] == M/P}, {Y, r}][[1]];
yStar = Y /. intersection;
rStar = r /. intersection;

(*均衡点を表示*)
Print["均衡国民所得 Y* = ", N[yStar]];
Print["均衡利子率 r* = ", N[rStar]];

(*グラフ描画範囲を指定*)
yMin = 1000;
yMax = 3000;

graph = Plot[Evaluate[{r /. isSol, r /. lmSol}], {Y, yMin, yMax}, 
  PlotRange -> {{yMin, yMax}, {0, 10}}, PlotStyle -> {Blue, Green}, 
  PlotLegends -> {"IS曲線", "LM曲線"}, AxesLabel -> {"Y（国民所得）", 
    "r（利子率）"},
  PlotLabel -> "IS-LMモデルにおける均衡（縦軸：利子率）", ImageSize -> Large, 
  Epilog -> {Red, PointSize[Large], Point[{yStar, rStar}], Black, 
    Text[Style["均衡点", 12], {yStar + 50, rStar + 0.3}]}]

(*PNG形式で保存*)
path = "/Users/macmini2025/Documents/\
Mathematica/";
filename = "ISLM_Equilibrium2.png";

(*ディレクトリが存在するかチェックして、存在すれば保存*)
If[
 DirectoryQ[path],
 Export[path <> filename, graph],
 Print["保存に失敗：ディレクトリが存在しません \[RightArrow] ", path]]
    

IS-LMモデルを表示

政府支出や減税などの財政政策は，総需要を増加させ，IS曲線を右方にシフトさせる．政府支出を，

\[ G = 300 \] と増加させることにする．(8)は， \[ Y = C + I + G = 100 + 0.8(Y - 100) + (200 - 10r) + \mathbf{300} \] \[ = 100 + 0.8Y - 80 + 200 - 10r + 300 = 0.8Y + 520 - 10r \] \[ 0.2Y = 520 - 10r \quad \Rightarrow \quad Y = 2600 - 50r \] と計算できる．ここから \[ Y = 2600 - 50r \tag{12} \] とIS曲線が計算できる．

均衡は IS = LM の交点として求められる．LM曲線（(11)）は変化しないので，(11)，(12)より，

\[ 2600 - 50r = 1600 + 80r \quad \Rightarrow \quad 1000 = 130r \] \[ \Rightarrow \quad r = \frac{1000}{130} = \frac{100}{13} \approx 7.692 \] \[ Y = 2600 - 50 \cdot \frac{100}{13} = \frac{28450}{13} \approx 2215.4 \] と計算できる．したがって，新しい均衡は \[ Y^{**} \approx 2215.4,\quad r^{**} \approx 7.692 \] となる．

表にまとめると以下のようになる．

状況	\( r \)（利子率）	\( Y \)（国民所得）	備考
初期	約 3.85	約 1907.5	基準
財政拡張	約 7.69	約 2215.4	金利上昇，国民所得上昇

IS-LMモデルの財政政策のアニメーションを表示

中央銀行が通貨供給量を増やすと、貨幣市場の均衡条件が変化し、LM曲線が右方にシフトする。ここでは、貨幣供給を

\[ M = 500 \] と増加させることにする。(5)，(7)をもとに、(10)式の右辺を変化させると、 \[ \frac{M}{P} = 0.25Y - 20r \Rightarrow 500 = 0.25Y - 20r \] \[ \Rightarrow \quad Y = 2000 + 80r \] よって、新しいLM曲線は以下のようになる： \[ Y = 2000 + 80r \tag{13} \]

IS曲線（(9)）は変化しないので、(9)，(13)より： \[ 2100 - 50r = 2000 + 80r \Rightarrow 100 = 130r \Rightarrow r = \frac{100}{130} = \frac{10}{13} \approx 0.769 \] この値を IS 曲線に代入して \( Y \) を求めると： \[ Y = 2100 - 50 \cdot \frac{10}{13} = \frac{26800}{13} \approx 2061.5 \]

よって、金融緩和後の新しい均衡は、 \[ r^{**} \approx 0.769,\quad Y^{**} \approx 2061.5 \] となる。

以下の表に、金融緩和による変化を整理する：

状況	\( r \)（利子率）	\( Y \)（国民所得）	備考
初期	約 3.85	約 1907.5	基準
金融緩和	約 0.77	約 2061.5	金利低下，国民所得増加

IS-LMモデルの金融政策アニメーションを表示